Theory for Exercise 5¶

Problem 1¶

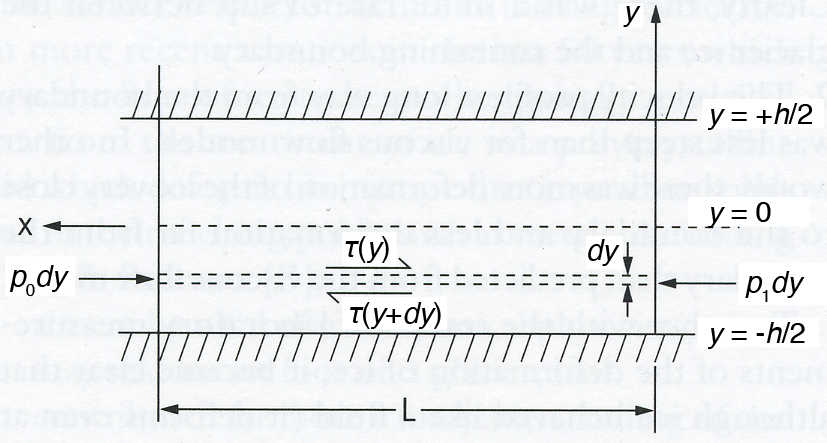
Figure 1. Schematic diagram of pressure-driven flow in a channel.

The viscosity of ice depends on both temperature and stress. For simplicity, we’ll consider the case where viscosity is only a function of shear stress. Consider a channel of width $h$ centered about $y = 0$, with lateral boundaries at $y = \pm h/2$ (Figure 1). A pressure gradient $\Delta p = p_{1} - p_{0}$ drives flow within the channel of length $L$. The shear stress in the fluid depends on the applied pressure gradient and the distance from the channel boundaries

\[\frac{d \tau}{d y} = \frac{d p}{d x} = \frac{p_{1} - p_{0}}{L} \tag{1}\]

where $\tau$ is the shear stress. We know that for Newtonian fluids

\[\tau = \eta \frac{d u}{d y} \tag{2}\]

where $\eta$ is the dynamic viscosity of the fluid. Substituting the right side of Equation 2 into the left side of Equation 1 we find

\[\eta \frac{d^{2} u}{d y^{2}} = \frac{d p}{d x} \tag{3}\]

Integrating Equation 3 with respect to $y$ twice we get

\[\begin{split}\begin{align} \int \frac{d^{2} u}{d y^{2}} &= \frac{1}{\eta} \int \frac{d p}{d x} \tag{Integrate once}\\ \frac{d u}{d y} &= \frac{1}{\eta} \frac{d p}{d x} y + c_{1} \tag{4} \\ \int \frac{d u}{d y} &= \frac{1}{\eta} \int \frac{d p}{d x} y + c_{1} \tag{Integrate again} \\ u(y) &= \frac{1}{2 \eta} \frac{d p}{d x} y^{2} + c_{1} y + c_{2} \tag{5} \end{align}\end{split}\]

Since we know $d u / d y = 0$ at $y = 0$, we find $c_{1} = 0$, and because we assume zero slip at the boundaries of the channel ($u = 0$ at $y = \pm h / 2$), $c_{2} = (1 / 2 \eta)(d p / d x)(h / 2)^{2}$. Thus,

\[u(y) = \frac{1}{2 \eta} \frac{d p}{d x} \left[ y^{2} + \left( \frac{h}{2} \right)^{2} \right] \tag{6}\]

This is the velocity profile for a Newtonian fluid, but as you will recall, we learned that ice is a non-Newtonian (nonlinear viscous) fluid. As such, the behavior should be modeled using a power-law, where the strain rate is a related to the shear stress as follows

\[\frac{d u}{d y} = a \tau^{n} \tag{7}\]

where $a$ is a function of the viscosity and temperature (we will ignore temperature for now), and $n$ is the power-law exponent. If we solve Equation 7 in terms of $\tau$, we can substitute the result into Equation 1 to get

\[a^{-1/n} \frac{d}{d y} \left( \frac{d u^{1/n}}{d y} \right) = -\frac{p_{1} - p_{0}}{L} \tag{8}\]

Assuming symmetry about the center line $y = 0$ and integrating we see

\[\begin{split}\begin{align} \int \frac{d}{d y} \left( \frac{d u^{1/n}}{d y} \right) &= -a^{1/n} \int \frac{p_{1} - p_{0}}{L} \tag{Integrate} \\ \frac{d u^{1/n}}{d y} &= -a^{1/n} \frac{p_{1} - p_{0}}{L} y + c_{1} \tag{Raise both sides to the power n} \\ \frac{d u}{d y} &= -a \left( \frac{p_{1} - p_{0}}{L} \right)^{n} y^{n} + c^{n}_{1} \tag{Apply BC $\frac{d u}{d y} = 0 \bigg\rvert_{y=0}$} \\ \frac{d u}{d y} &= -a \left( \frac{p_{1} - p_{0}}{L} \right)^{n} y^{n} \tag{9} \end{align}\end{split}\]

Note

In the derivations, boundary condition has been abbreviated as BC to save space.

Now integrate Equation 9 and assume $u = 0$ at $y = \pm h / 2$.

\[\begin{split}\begin{align} \int \frac{d u}{d y} &= -a \left( \frac{p_{1} - p_{0}}{L} \right)^{n} \int y^{n} \\ u(y) &= -\frac{a}{n + 1} \left( \frac{p_{1} - p_{0}}{L} \right)^{n} y^{n + 1} + c_{2} \tag{Apply BC $u = 0$ at $y = \pm \frac{h}{2}$} \\ u(y) &= \frac{a}{n + 1} \left( \frac{p_{1} - p_{0}}{L} \right)^{n} \left[ \left( \frac{h}{2} \right)^{n + 1} - y^{n + 1} \right] \tag{10} \end{align}\end{split}\]

The mean velocity in the fluid is

\[\begin{split}\begin{align} \bar{u} &= \frac{2}{h} \int_{0}^{h/2} u dy \\ &= \frac{a}{n + 2} \left( \frac{p_{1} - p_{0}}{L} \right)^{n} \left( \frac{h}{2} \right)^{n + 1} \tag{11} \end{align}\end{split}\]

We can calculate a non-dimensional velocity now by dividing the velocity at any point in the channel by the mean velocity

\[\frac{u}{\bar{u}} = \left( \frac{n + 2}{n + 1} \right) \left[ 1 - \left( \frac{2 y}{h} \right)^{n + 1} \right] \tag{12}\]

Problem 2¶

Figure 2. Schematic diagram of a viscous fluid flowing down an inclined plane.

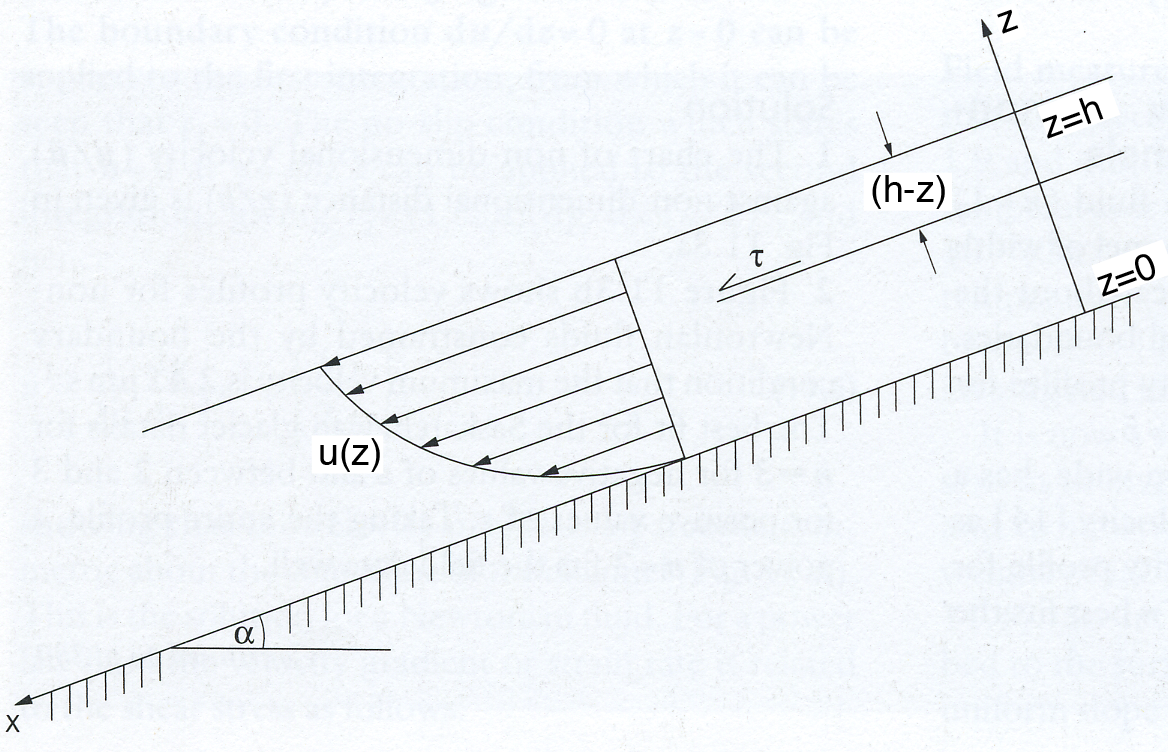
The velocity of a fluid flowing down an inclined plane can be modelled using some basic physical relationships. First, recall that the basal shear stress for a fluid flowing down an inclined plane is due to the down slope component of the weight of the overlying fluid

\[\tau = \rho g h \sin{\alpha} \tag{13}\]

where $\rho$ is the fluid density, $g$ is the acceleration due to gravity, $h$ is the thickness of the fluid perpendicular to the inclined plane and $\alpha$ is the angle of the plane with respect to horizontal. At any distance $z$ above the bed

\[\begin{split}\begin{align} \tau &= \rho g (h - z) \sin{\alpha} \\ &= \gamma_{x} (h - z) \tag{14} \end{align}\end{split}\]

where $\gamma_{x} = \rho g \sin{\alpha}$ is the downslope component of the gravitational force. Combining Equation 2 from Part 1 of the theory with Equation 14 we find the constitutive equation for a Newtonian fluid is

\[\frac{d u}{d z} = \frac{\gamma_{x} (h - z)}{\eta} \tag{15}\]

Integrating Equation 15 yields

\[\begin{split}\begin{align} \int \frac{d u}{d z} &= \int \frac{\gamma_{x} (h - z)}{\eta} \\ u(z) &= \frac{\gamma_{x}}{\eta} \left( z h - \frac{z^{2}}{2} \right) + c_{1} \tag{16} \end{align}\end{split}\]

where $c_{1} = 0$ from the boundary condition $u = 0$ at $z = 0$. Equation 16 can be rewritten as

\[u(z) = \frac{1}{2} \left( \frac{\gamma_{x}}{\eta} \right) \left[ h^{2} - (h - z)^{2} \right] \tag{17}\]

For a non-Newtonian fluid, Equation 14 can be modified to account for the case where the strain rate varies as a power of the shear stress (Equation 7 from Part 1 of the theory)

\[\frac{d u}{d z} = a \left[ \gamma_{x} (h - z) \right]^{n} \tag{18}\]

To determine the velocity profile, we need to integrate Equation 18. If we use the boundary condition that the basal sliding velocity is equal to ub rather than zero, we get

\[\begin{split}\begin{align} \int \frac{d u}{d z} &= a \int \left[ \gamma_{x} (h - z) \right]^{n} \\ u(z) &= u_{\mathrm{b}} + \frac{a}{n + 1} \gamma_{x}^{n} \left[ h^{n + 1} - (h - z)^{n + 1} \right] \tag{19} \end{align}\end{split}\]