Viscous flow down an incline¶
Goals¶
- Present the equations of linear viscous flow down an inclined plane
Linear viscous flow¶
Shear stress in the fluid¶
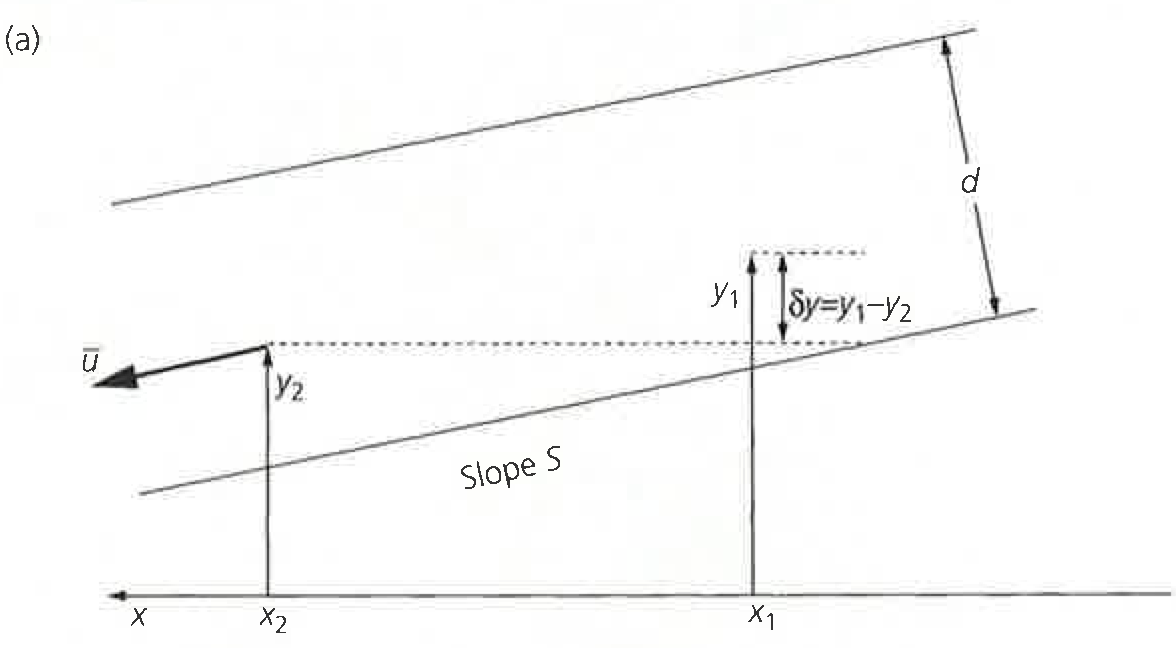
For a fluid flowing down an inclined slope, the change in potential energy per unit area of the contact surface along some length of the slope \(\delta x\) is
where \(\Delta E_{\mathrm{P}}\) is the change in potential energy, \(\rho\) is the fluid density, \(g\) is the acceleration due to gravity, \(h\) is the thickness of the flow, \(\delta z\) is the elevation change over the distance \(x\), \(\bar{u}\) is the average flow velocity, and \(S\) is the slope of the incline.
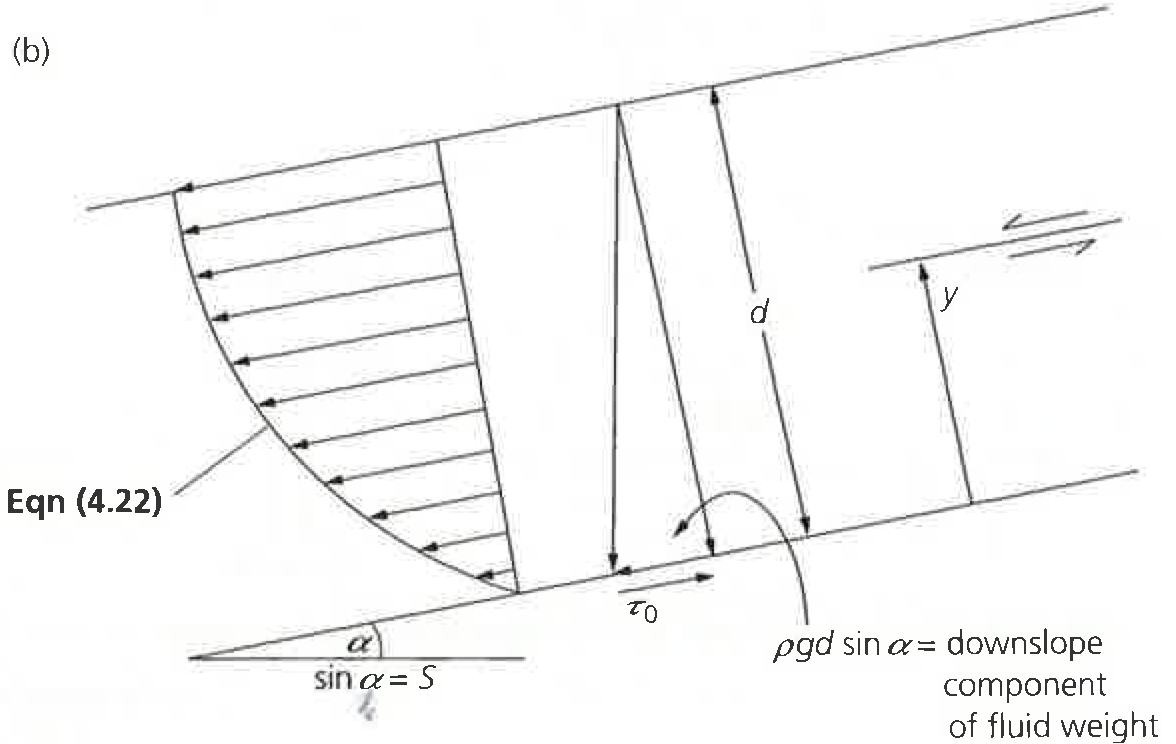
The downslope component of the gravity force on the flow is thus \(\rho g h S\), which must be opposed by the drag force at the base of the flow \(\tau_{0}\). Thus, we can say
We can also calculate the shear stress for any position \(z\) above the base of the flow, which is a function of the thickness of the overlying fluid \((h - z)\)
Attention
What does this suggest about the shear strength as a function of depth in the fluid?
Linking to viscous flow¶
For a laminar flow, we know \(\tau = \eta du/dz\), so we can rewrite the resistance equation as
If we integrate this equation with respect to \(z\), we find
If we assume the flow velocity \(u = 0\) at \(z = 0\) (the base of the flow), the constant \(c_{1} = 0\), so we are left with
Attention
- What would the velocity profile look like in this flow?
- Where is the maximum velocity?
- What happens if the viscosity decreases? Slope increases? Thickness increases?
Viscous flow take-home messages¶
- The flow is a balance between the gravitational force on the fluid and resistance (drag) at the base
- The flow velocity increases following a parabolic geometry from \(u = 0\) at the base to \(\frac{\rho g S}{\eta} \frac{z^{2}}{2}\)
Caveats¶
- Steady-state
- 1-D
- Laminar flow!
- Constants are constant
- No temperature dependence